最近想使用免费的LTSPICE做一些简单的信号仿真,评估信号经过一些链路模型传输后信号SI表型如何?需要在LTSPICE中采用信号系统中通常采用的伪随二进制码序列(PRBS)作为信号激励,模拟真实传输场景下数字信号频谱分布,同时在链路的接收端将信号切片叠成眼图形式对接收到的方波信号质量做比较直观的评估。但是如果采用LTSPICE中自带的移位寄存器设计数字电路来实现这个功能,整体的模拟时间会比较长,同时产生长序列高速率的PRBS比较困难。为提高模拟效率并简化仿真电路,所以信号采用导入PRBS的PWL file来实现。
PWL文件的产生
PRBS(伪随机二进制序列)简介
Pseudo-Random Binary Sequence,伪随机二进制序列的产生一般依靠数字电路的移位寄存器来实现。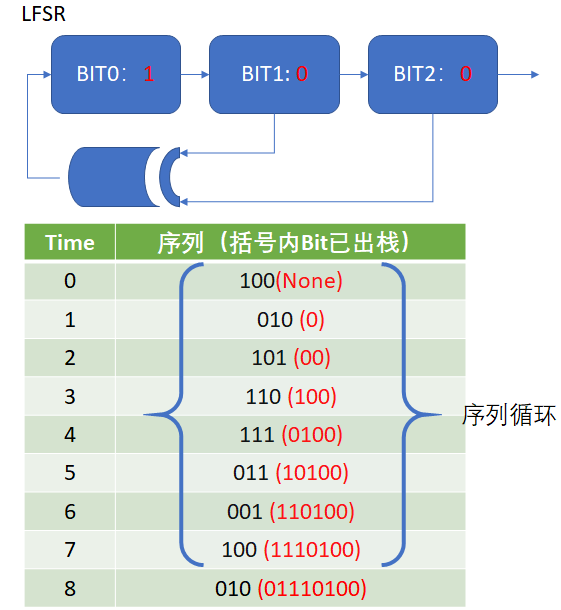
从上图中我们可以得到一些信息:
1、n阶PRBS的码型长度是2^n-1,图中第7次运算已经重复了time 0的情况,所以0~6是一个标准的循环,第7次已出栈的模型长度是7个
2、从右到左,最先出栈的n个码型对应的是LFSR的初始寄存器值,后文对应seed值;
3、对于PRBS n来说,其中最长有n个连续的1或者0,对应n-1个连续的0或者1;
对于具体的PRBS特征可以查阅对应资料深入了解,后续对他的频谱、功率谱、Mark ration概念再做进一步学习。
构建一个函数实现通信常用的N阶PRBS信号
详见代码和代码注释1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45#############################################################################################
# function: 产生通信测试用PRBS伪随机序列
# 入口参数:
# 1、User_defined/PRBS_N (N=7,9,11,15,17,20,23,29,31)--使用自定义或者规定的PRBS_N序列;
# 2、seeds--产生伪随机序列的种子;
# 3、polynomial tap--规定的伪随机序列的标准tap;x^tap1+x^tap2+1 tap1>tap2
# 参数使用字典来传递
# 返回参数:
# 对应的PRBS码型
#############################################################################################
# seed 文件只作为参考,后续可根据对应协议更正
prbs_dictionary={"PRBS_7":['0101010',[7,6]],
"PRBS_9":['010101010',[9,5]],
"PRBS_11":['01010101010',[11,9]],
"PRBS_15":['010101010101010',[15,14]],
"PRBS_17":['01010101010101010',[17,14]],
"PRBS_20":['10101010101010101010',[20,3]],
"PRBS_23":['01010101010101010101010',[23,18]],
"PRBS_29":['01010101010101010101010101010',[29,27]],
"PRBS_31":['0101010101010101010101010101010',[31,28]],
}
# if prbstype=PRBS_N, default of seed and taps are None,
# if prbstype=User_defined, seed and taps must be given
def prbs_Generator(prbstype, seed = None, taps = None):
if prbstype == 'User_defined':
prbs_sequence = prbs_create(seed,taps)
else:
prbs_sequence = prbs_create(prbs_dictionary.get(prbstype)[0],prbs_dictionary.get(prbstype)[1])
return prbs_sequence
def prbs_create(seed, taps):
#传入的字符串转化为列表
sequence_list = [int(i) for i in list(seed)]
#获得对应的PRBS周期长度
prbs_length = (2 << (len(seed) - 1))-1
#产生定义长度的伪随机序列
for i in range(prbs_length):
# 对taps规定的bit位置进行异或计算
mod_two_add = sum([sequence_list[t-1] for t in taps])
xor = mod_two_add % 2
#计算出的Bit值插入到队列首端
sequence_list.insert(0, xor)
#list 倒置
sequence_list.reverse()
return sequence_list
将PRBS信号转换成标准模拟用的PWL文件
LTSPICE的PWL文件格式如下,第一行的表头不体现,其他行多是时间参数对应的电平电压
|time|Voltage|
|:—-:|:—-:|
|时间|电平电压|
转换过程涉及将Bit序列转换成逻辑电平,在逻辑电平转换过程中引入上升、下降时间、Bit Rate(bit period的倒数)等常见定义,转换过程详见下述代码。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40#############################################################################################
# function: 通过特定的PRBS产生PWL文件
# version: V1.0
# 入口参数:
# 1、输入PWL文件需要的Bit, V0(低电平), V1(高电平), Bit rate, Rise time, Fall time;
# 返回参数:
# 输出符合spice仿真需要的PWL文件(当前为time 与 waveform对应的dictionary)
#############################################################################################
def create_PWL(Bits, V0, V1, BitRate, RiseTime, FallTime):
#从逻辑level转换成电平幅度
waveform_list = []
time_list = []
volt_Bits = []
# print len(Bits)
# print range(len(Bits))
for i in range(len(Bits)):
if Bits[i] == 1:
volt_Bits.append(V1)
else:
volt_Bits.append(V0)
# 装换成含上升,下降时间的电平幅度
for bitN in range(len(Bits)):
waveform_list.append(volt_Bits[bitN])
waveform_list.append(volt_Bits[bitN])
# 获取精准的浮点运算,先将数字转换成字符使用Decimal计算后,再转回float类型
bit_Period = round(1.0/BitRate, 3)
for time in range(len(waveform_list)-1):
if time%2 == 1:
if waveform_list[time] > waveform_list[time+1]:
time_list.append(float(Decimal(str(time+1))/Decimal('2')*Decimal(str(bit_Period))-Decimal(FallTime)))
else:
time_list.append(float(Decimal(str(time+1))/Decimal('2')*Decimal(str(bit_Period))-Decimal(RiseTime)))
else:
time_list.append(float(Decimal(str(time))/Decimal('2')*Decimal(str(bit_Period))))
pwl_List = {"time":time_list, "Waveform":waveform_list}
return pwl_List
其中关键点时使用到了Decimal函数,代码运用过程中发现,计算机采用二进制对浮点数进行表示和运算会出现计算精度丢失的情况,哪怕是0.2-0.1的计算,也会出现莫名的精度丢失,所以采用python中Decimal函数克服。
The decimal module provides support for fast correctly-rounded decimal floating point arithmetic. It offers several advantages over the float datatype:
Decimal函数解释, 参见python手册
将产生的PWL字典文件写入TEXT文档
上文已经可以产生需要的PWL文件,但是为了模拟仿真的方便性,我们需要将产生的PWL数据写入Text文档中,然后在LTSPICE仿真时直接引入,下面是存储的代码文件1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16#############################################################################################
# function:将生成的pwl_List按照标准格式写入text文档中,第一列为time, 第二列为voltage
# version: v1.0
# 入口:
# 1、pwl_list; 标准波形存储的字典
# 2、savePath_Name; 文件保存路径和名称
# 出口:
# 标准格式保存的text文档
#############################################################################################
def save_PWL_File(pwl_list, savePath_Name):
DataFile = open(savePath_Name, mode = 'w+')
for i in range(len(pwl_list.get("time"))):
content = str(pwl_list.get("time")[i]) + ' ' + str(pwl_list.get("Waveform")[i]) + '\n'
DataFile.writelines(content)
DataFile.close()
使用下面的代码生成一个测试文件来进行仿真测试1
2
3
4result_data = prbs_Generator(prbstype = "PRBS_9")
savePath_Name = ".\pwl.txt"
pwl_file = create_PWL(result_data, 0, 5, BitRate = 10, RiseTime = 0.01, FallTime = 0.02)
save_PWL_File(pwl_file, savePath_Name)
运行代码后可以产生一个pwl.txt文档,其中部分信息如下图
LTSPICE仿真测试
首先构建如下图的仿真电路,假设信号源的阻抗是25ohm,高速线的阻抗为25ohm,负载采用RLC模型代替,其阻抗跟随频率变化。
导入PWL的设置如下
仿真设置中比较关键的利用.option baudrate让仿真软件自动在结果测生成眼图,软件运行的仿真结果如下,生成了比较漂亮的眼图,同时源的方波也比较正常
源的waveform